RESÚMENES
Cursos
Pierre Bayard (UNAM)
Superficies de curvatura constante en el espacio de Minkowski
Resumen: Es bien conocido que las superficies completas de curvatura de Gauss K=1 en el espacio euclidiano de dimensión 3 son las esferas unitarias. La situación es muy distinta en el espacio de Minkowski. El objetivo principal del mini-curso será presentar la clasificación de las superficies enteras de K=-1 en el espacio de Minkowski de dimensión 3. Este resultado usa métodos de geometría y análisis, especialmente funciones armónicas del plano complejo al plano hiperbólico y ecuaciones de Monge-Ampère en dimensión 2. Ha sido obtenido recientemente por F. Bonsante, A. Seppi y P. Smillie (después de trabajos de Li, Guan, Jian y Schoen, entre otros).
Claudio Meneses (Universidad de Kiel)
El espacio de Eguchi–Hanson: paradigma de la geometría hiperkähler
Resumen: Desde el inicio de su estudio formal hace poco más de cuatro décadas, las variedades hiperkähler se consolidaron rápidamente como objetos geométricos de gran interés. Su profunda riqueza estructural las posiciona como un puente común entre la geometría diferencial, la geometría algebraica y la física matemática, disciplinas en las que fueron introducidas de manera independiente y casi simultánea. Un ejemplo primigenio, explícito y a la vez no-trivial es el llamado espacio de Eguchi–Hanson, que fuera introducido de manera simultánea por Calabi y Eguchi–Hanson en 1979. El objetivo de este curso es el de servir como una brevísima invitación a las variedades hiperkähler y sus principales modelos y constructos geométricos (haces cotangentes holomorfos, órbitas coadjuntas complejas, cocientes hiperkähler, espacios de twistores), usando al espacio de Eguchi–Hanson como modelo de juguete de aquellos. Los requisitos son conocimientos básicos de variable compleja y geometría diferencial, así como de grupos y álgebras de Lie.
Raquel Perales (UNAM-Cimat)
De las variedades a las corrientes
Resumen: En este minicurso se estudiará la medida de Hausdorff, el teorema de diferenciación de funciones Lipschitz, la noción de conjuntos rectificables. Concluiremos definiendo a las corrientes, generalizaciones de variedades riemannianas orientables, y mencionaremos algunas de sus aplicaciones.
Bibliografía:
-Lectures on Geometric Measure Theory. Leon Simon. Proceedings of
The Centre for Mathematical Analysis, Australian National University,
Volume III, 1983.
-Currents in metric spaces. Luigi Ambrosio y Bernd Kirchheim. Acta
Mathematica volume 185,(2000)
Charlas
Gil Bor (CIMAT)
Cúspides de cáusticas por reflexión
Resumen: Colocando una fuente de luz dentro de una mesa de billares convexa (o espejo), la n-ésima cáustica por reflexión es la envolvente de los rayos de luz después de n reflexiones. Theorema: para una ubicación genérica de la fuente de luz, cada una de estas cáusticas tiene por lo menos 4 cúspides. Conjetura: son exactamente 4 cúspides si y sólo si la mesa es una elipse y la fuente de luz no es uno de los focos. Aqui estan la 2nda, 5ta y 8va cáusticas en una elipse (marcando las 4 cúpides con discos grises, la fuente de luz con un disco blanco y los 2 focos con puntos negros).
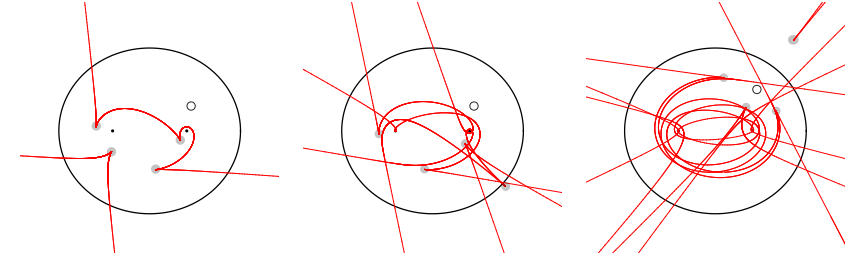
Esta es la versión de billares de un teorema de Carathéodory (1912) acerca del número de cúspides de la caústica (curva de puntos conjugados) de un punto en una superficie cerrada convexa y la "Última afirmación geométrica de Jacobi" (1842) acerca de la cáustica de un punto no umbílico de una elipsoide triaxial, demostrada para n=1 en 2004. (Trabajo en colaboración con Serge Tabachnikov, Penn State USA). Ver artículo.
Padi Fuster (Universidad de Colorado, Boulder)
La restricción del operador de Laplace en variedades Riemannianas
Resumen: En una variedad Riemanniana, no existe un operador de Laplace canónico para campos o formas diferenciales, y no está claro cuál es el laplaciano "correcto" a utilizar al formular ecuaciones de dinámica de fluidos. En esta charla, analizaremos diferentes enfoques para obtener un operador de viscosidad al considerar una subvariedad de Riemann en $\mathbb{R}^n$. Además presentaremos algunos ejemplos concretos utilizando la reciente extensión de la fórmula de Gauss para el operador de Laplace en hipersuperficies por Chan y Czubak (2023). Finalmente, presentaremos resultados preliminares sobre la derivación de un operador de viscosidad intrínseca en un elipsoide utilizando una heurística del límite de capa delgada.
Ana Karla García (UNAM)
Espacios moduli de métricas riemannianas planas sobre variedades cerradas
Resumen: Se hablará sobre variedades cerradas que admiten una métrica riemanniana con curvatura seccional constante igual a cero, las cuales se pueden relacionar con grupos discretos llamados grupos de Bieberbach. Usando estos grupos podemos describir a los espacios moduli de métricas planas sobre variedades cerradas. Daremos algunos resultados para cuando la dimensión de la variedad sea baja.
Josué Meléndez (UAM)
Rigidez de hipersuperficies con curvatura media constante de orden superior
Resumen: Consideramos una hipersuperficie M con curvatura media de orden superior Hr constante en una forma espacial con dos curvaturas principales diferentes lambda, mu de multiplicidad (n-1,1) respectivamente. Probamos que la curvatura de Ricci en alguna dirección especial no cambia de signo si y sólo si M es isoparamétrica, generalizando algunos resultados previos. Por otro lado, exhibimos una familia entera de hipersuperficies en la esfera unitaria con Hr constante y con curvatura de Gauss-Kronecker sin cambiar de signo.
Matías Navarro (UADY)
Geometría de hipersuperficies nulas inmersas en variedades lorentzianas.
Resumen: En esta charla hablaremos acerca de algunos resultados de clasificación de hipersuperficies nulas (o tipo luz) M inmersas en espacios modelo lorentzianos provistas de cierta distribución "screen" que refleja hasta cierto punto la geometría de M. Estos resultados se obtuvieron en colaboración con Didier Solís y Oscar Palmas en los años 2019-2023.
Jesús Núñez Zimbrón (UNAM)
Clasificación de espacios generalizados de Seifert
Resumen: Los espacios de Alexandrov son espacios métricos (no necesariamente suaves) que admiten una noción de "curvatura seccional acotada por debajo". En este contexto, se conoce como "colapso" al fenómeno en el que se tiene una sucesión de espacios de Alexandrov de cierta dimensión fija que converge (en la topología de Gromov-Hausdorff) a otro espacio de Alexandrov de dimensión estrictamente menor. Este fenómeno está relacionado con otros importantes como la existencia de acciones de grupos y teoremas de geometrización. En esta plática hablaré de una clasificación simbólica de los llamados espacios generalizados de Seifert de dimensión 3, que aparecen naturalmente en el colapso de espacios de Alexandrov y como piezas fundamentales de la geometrización de espacios de Alexandrov tridimensionales. Este es un trabajo en conjunto con Fernando Galaz García.
Oscar Palmas (UNAM)
Subvariedades seudo-paralelas y $\lambda$-isotrópicas
Resumen: Las inmersiones seudo-paralelas son una generalización de las inmersiones con segunda forma fundamental paralela. Consideramos este concepto cuando el espacio ambiente es una variedad semi-riemanniana. En el caso de una inmersión tipo tiempo en una forma espacial semi-riemanniana de dimensión 4, el concepto de seudo-paralelismo es equivalente a ser $\lambda$-isotrópico. En la segunda parte de nuestra charla analizaremos el concepto de $\lambda$-isotropía para subvariedades nulas en formas espaciales lorentzianas.
Éste es un trabajo conjunto con Guillermo Lobos, Minor Melara (Universidade Federal de São Carlos, Brasil) y Theophile Kemajou (Université de Maroua, Camerún).
Juan Miguel Ruiz (UNAM)
Cotas inferiores para el perfil isoperimétrico y el invariante de Yamabe
Resumen: Hablaremos sobre algunas cotas inferiores explícitas para el perfil isoperimétrico de variedades que son el producto Riemanniano entre una variedad compacta $M^n$ y el espacio Euclideano con la métrica plana, $(M^m\times \mathbb{R}^n,g+g_E)$, $m,n>1$. Hablaremos también sobre algunas aplicaciones de estos resultados que mejoran las cotas inferiores conocidas del invariante de Yamabe de ciertas variedades. Este es un trabajo conjunto con Areli Vázquez Juárez.
Gabriel Ruiz
¿Por qué las variedades Nearly Kahler existen a partir de dimensión seis?
Resumen: Las variedades Casi Complejas forman una familia muy grande de variedades Riemannianas. Dentro de esa familia destacan las variedades Kahler y las variedades Nearly Kahler. En esta charla daremos los conceptos básicos de variedades Nearly Kahler desde el punto de vista de Geometría Riemanniana. Vamos a ver por qué dichas variedades existen a partir de la dimensión seis. Veremos ejemplos de tales variedades como S 6. Y en particular vamos a describir la construcción de Sekigawa de una estructura Nearly Kahler en el grupo de Lie producto G × G donde G es un grupo de Lie con métrica Riemanniana bi-invariante. Esta charla esta inspirada, en parte, en el trabajo conjunto con Rodrigo Aguilar durante su maestría y doctorado.

